1985年,为了节省当时出现故障的苏联空间站的致敬7,两名宇航员被派去进行紧急维修。完成任务后,一名宇航员詹尼贝科夫(Janibekov)打开了从地球上带来的物资。这些物资用机翼螺母锁定,珍妮贝科夫(Janibekov)在松动时会定期发现至180度,并继续在空间站上漂浮并旋转。后来,这种现象被称为Janibekov效应。

实际上,我们可以再现这种对地球的影响。以网球球拍为例,我们人为地设置了垂直于彼此的三个主轴:一个是沿着手柄的主轴,另一个是垂直于手柄和网平面的主轴,而第三个则垂直于手柄和网的主轴。当我们让网球球拍围绕一个或三个主轴旋转并将其扔到空中时,球拍的旋转是稳定的,并且仅围绕初始轴旋转。当我们让网球拍围绕两个主轴旋转并将其扔到空中时,它的运动不稳定,最终将演变成大约三个轴的旋转。因此,Janibekov效应也称为网球拍效应或中间轴效应。

1991年,一篇公开发表的文章解释了这一效果。我还阅读了一些流行的科学文章和视频,以解释这种效果。他们要么用纯文本解释,要么直接给出欧拉的动力学方程式以进行解释。今天,我们通过得出Euler动力学方程来逐渐解释这种效果。
Euler的动力学方程推导
首先,我们需要知道时刻和角动量之间的关系。如果您忘记了,那么我们可以回想起力量与动量之间的关系:力与动量与时间的导数相同。同样,力矩等于角动量与时间的衍生物。
方程的左侧是M矩M,我们可以直接编写其组件形式。

方程式的右侧是角动量反对时间的衍生物。尽管其计算更为复杂,但我们仍然可以编写组件表格。
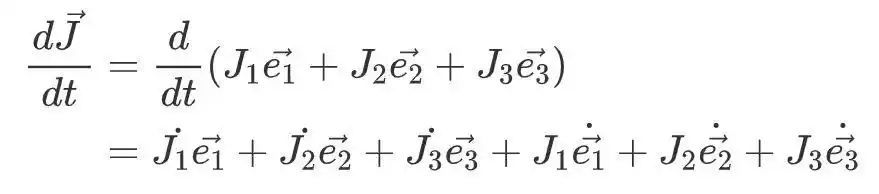
接下来,这里有一个问题。最后三个术语是基本向量随着时间的变化的变化,它们取决于我们采用的坐标系。在这里,我们要采用的是刚体坐标系统。在刚体坐标系中,基本矢量随刚体的旋转而旋转,因此随时间的基本矢量的变化是角速度ω越过基本向量。如果您还不了解它,您可以考虑如何在高中得出循环运动的加速度。
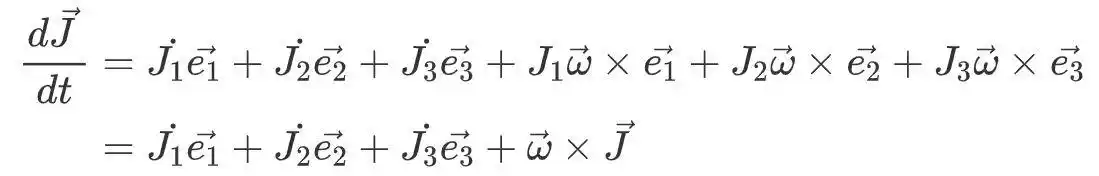
根据矢量交叉乘法定律,我们可以以以下形式编写最后一项。
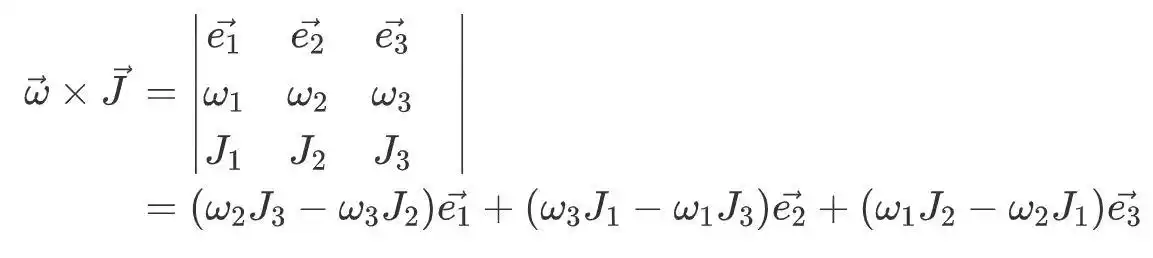
现在,整个公式变得非常复杂,但是如果我们替代角动量,角速度和惯性矩之间的关系,则该公式就会变得非常简单。在惯性纺锤的时刻,惯性矩不会随旋转而变化。我们有以下关系:
将其替换为上述公式,我们最终将获得此结果:
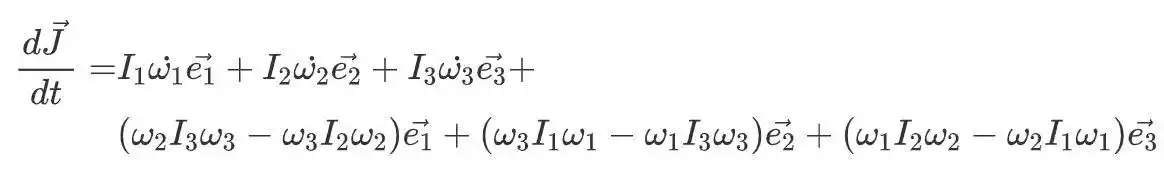
最后,我们使每个组件的力矩和每个组件的角动量等于时间,并且获得了著名的Euler动力学方程。
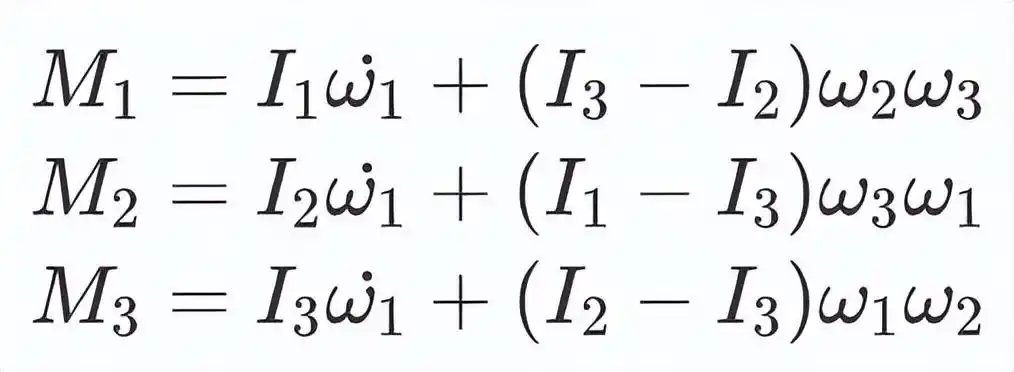
网球拍效果的解释

解释网球拍效应的一个重要点是理论与现实之间的差距。从理论上讲,我们可以使网球球拍围绕任何轴稳定旋转,而其他两个轴的角速度始终为零。但是实际上,我们无法做到这一点,总会有一些干扰破坏这种理想状态。现在,我们要研究的是,在轻微干扰后是否会放大干扰。
我们假设惯性1>惯性矩2>惯性矩3的时刻,网球球拍被扔到空中后没有扭矩。首先,我们研究了围绕主轴1的旋转。目前,ω1是恒定的,其时间的导数基本上为零,而ω2和ω3受到干扰,并且发生了轻微的角速度。现在,得出Euler动力学方程的第二个方程并将第三个方程式替换为其中,我们可以得到:
根据惯性时刻的大小,我们可以知道k
但是,当围绕主轴2旋转时,我们可以得到相同的原理:
在这一点上,我们知道k> 0,因此扰动将被放大,角速度将增加。也就是说,主轴2的旋转不稳定,小小的干扰会导致网球球拍翻转。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请联系本站,一经查实,本站将立刻删除。如若转载,请注明出处:http://www.sshk56.com/html/tiyuwenda/9666.html






